Số chính phương là gì? Định nghĩa, tính chất và ứng dụng trong toán học

“`html

Số Chính Phương là gì?

Số chính phương là một khái niệm quan trọng trong toán học, đặc biệt đối với các học sinh. Trong bài viết này, chúng ta sẽ cùng nhau tìm hiểu về số chính phương, từ định nghĩa cho đến các tính chất và ứng dụng của nó trong cuộc sống hàng ngày.

1. Giới thiệu chung về số chính phương

Trong toán học, số chính phương là một khái niệm cơ bản và quan trọng, thường xuất hiện trong chương trình học từ tiểu học đến trung học. Mục tiêu của bài viết là giúp người đọc hiểu rõ về định nghĩa số chính phương, các tính chất, cách nhận biết và ứng dụng của số chính phương.

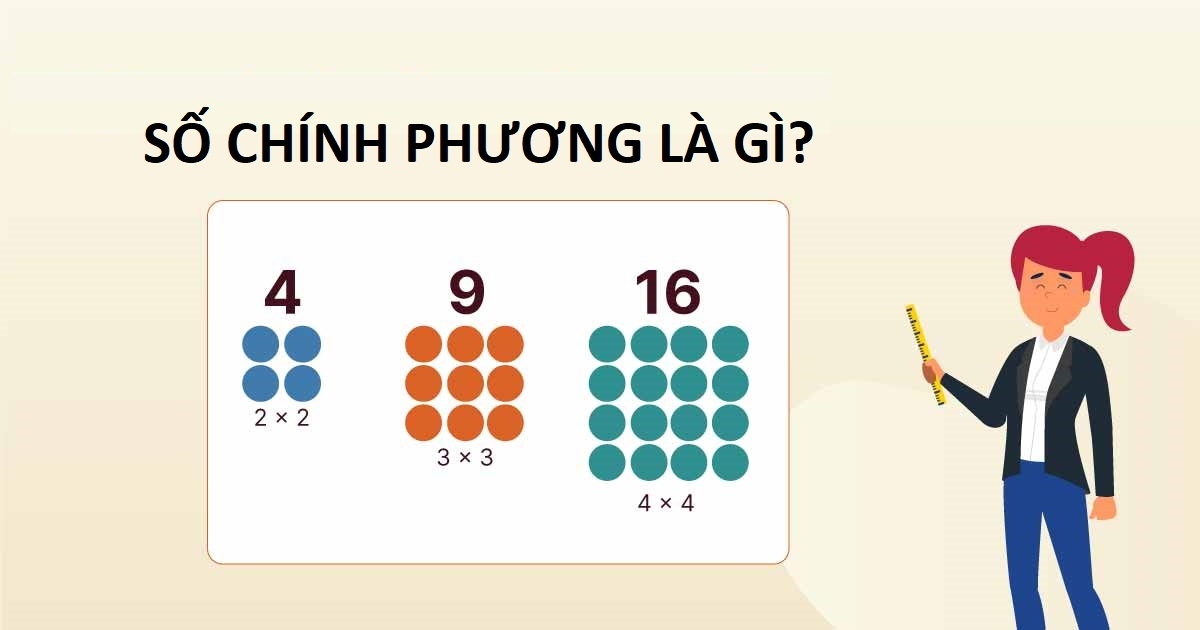
2. Số chính phương là gì?

Định nghĩa số chính phương

Số chính phương là một số tự nhiên được tính bằng bình phương của một số tự nhiên khác. Nói một cách đơn giản, nếu n là số chính phương, thì nó có thể được viết dưới dạng:

n = k²

trong đó k là một số tự nhiên.

Các số chính phương

Các số chính phương đầu tiên mà bạn có thể gặp là:

• 1 (1²)
• 4 (2²)
• 9 (3²)
• 16 (4²)
• 25 (5²)

Đây đều là những ví dụ tiêu biểu cho khái niệm số chính phương. Các ví dụ số chính phương này giúp tạo nền tảng cho việc hiểu sâu hơn về chủ đề.

3. Tính chất số chính phương

Số chính phương có một số tính chất đặc trưng mà chúng ta cần biết:

• Tận cùng số: Số chính phương chỉ có chữ số tận cùng là 0, 1, 4, 5, 6, hoặc 9. Nó không bao giờ có tận cùng bằng 2, 3, 7, hay 8.
• Phân tích thừa số nguyên tố: Trong phân tích thành thừa số nguyên tố, mọi số chính phương chỉ chứa các thừa số với số mũ chẵn.
• Biểu diễn dạng toán học: Số chính phương có thể được viết dưới dạng 4n hoặc 4n+1 nhưng không bao giờ ở dạng 4n+2, 4n+3, hoặc 3n+2. Những tính chất số chính phương này rất quan trọng trong việc nhận diện các số này trong toán học.

4. Ví dụ về số chính phương

Để hiểu rõ hơn về số chính phương, hãy cùng điểm qua một số ví dụ cụ thể:

• Số chính phương đầu tiên: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100.

Cách xác định số chính phương

Để xác định một số có phải là số chính phương hay không, bạn có thể thực hiện như sau:

• Lấy căn bậc hai: Nếu √n là một số tự nhiên, thì n là số chính phương. Ví dụ: 36 là số chính phương vì √36 = 6.

5. Cách nhận biết số chính phương

Các phương pháp dưới đây sẽ giúp bạn dễ dàng nhận biết số chính phương:

• Sử dụng máy tính: Tính căn bậc hai và kiểm tra xem kết quả có phải là số nguyên không.
• Sử dụng tận cùng số: Các số có chữ số tận cùng là 2, 3, 7, 8 không thể là số chính phương.
• Phân tích thừa số nguyên tố: Kiểm tra nếu số đó có thể được biểu diễn với các thừa số có số mũ chẵn. Việc biết cách nhận biết số chính phương sẽ giúp bạn vận dụng tốt hơn trong các bài toán.

6. Bài toán số chính phương

Để rèn luyện kỹ năng nhận biết và làm việc với số chính phương, bạn có thể thử những bài toán thú vị sau:

• Chứng minh một số là số chính phương: Tìm điều kiện để một biểu thức toán học là số chính phương.
• Ví dụ bài toán: Chứng minh rằng A = (x+y)(x+2y)(x+3y)(x+4y) là số chính phương. Đây là một bài toán số chính phương điển hình giúp củng cố kiến thức.

7. Ứng dụng của số chính phương

Số chính phương không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tiễn trong đời sống:

• Trong hình học: Số chính phương biểu thị diện tích của hình vuông khi biết cạnh là số nguyên.
• Trong mật mã học: Một số thuật toán mã hóa sử dụng số chính phương trong quá trình tính toán.
• Trong khoa học và kỹ thuật: Số chính phương được áp dụng để giải quyết bài toán liên quan đến lập phương trình và tối ưu hóa. Ứng dụng số chính phương rất đa dạng và hữu ích trong nhiều lĩnh vực.

8. Bảng số chính phương

Dưới đây là bảng danh sách các số chính phương từ 1 đến 10:

Số tự nhiên (n)	Số chính phương (n2)
1	1
2	4
3	9
4	16
5	25
6	36
7	49
8	64
9	81
10	100

Bảng số chính phương này giúp bạn dễ dàng tham khảo và ghi nhớ hơn.

9. Phân tích số chính phương

Khía cạnh hình học

Số chính phương có thể được hình dung qua các khía cạnh hình học, như việc xếp các điểm thành một hình vuông hoàn hảo. Phân tích số chính phương sẽ giúp các khái niệm liên quan trong toán học trở nên sinh động hơn.

Mối quan hệ với các khái niệm khác

Số chính phương tương tác chặt chẽ với số nguyên tố, tính chia hết và các dạng số tự nhiên khác, từ đó tạo ra một mạng lưới phong phú các mối liên hệ trong toán học.

10. Kết luận

Tóm lại, số chính phương là một phần quan trọng của toán học với những tính chất và ứng dụng đa dạng. Bài viết đã khám phá các khía cạnh cơ bản, từ định nghĩa đến ứng dụng thực tiễn, giúp người đọc không chỉ hiểu rõ về số chính phương mà còn biết cách áp dụng kiến thức của mình trong thực tế. Hãy tìm hiểu thêm và khám phá thế giới toán học đầy thú vị này!

Với những từ khóa phụ đã được bổ sung, bài viết trở nên phong phú hơn và dễ dàng cho người đọc tìm kiếm thông tin liên quan về số chính phương.

“`