Trực tâm là một khái niệm vô cùng quan trọng trong hình học, đặc biệt trong lĩnh vực toán học và vật lý. Hiểu rõ về trực tâm không chỉ giúp học sinh nắm bắt tốt hơn các khái niệm cơ bản mà còn mang lại nhiều ứng dụng thực tiễn trong đời sống và kỹ thuật. Bài viết dưới đây sẽ cung cấp cho bạn một cái nhìn tổng quát và chi tiết về trực tâm, từ định nghĩa, tính chất, ứng dụng cho đến cách tìm và phân loại.

Định nghĩa trực tâm
Trực tâm là một điểm quan trọng trong tam giác mà ai cũng cần phải hiểu. Theo định nghĩa trực tâm, đây chính là giao điểm của ba đường cao trong tam giác. Mỗi đường cao được vẽ từ một đỉnh của tam giác tới cạnh đối diện và vuông góc với nó. Để hình dung cụ thể, khi bạn vẽ một tam giác và kẻ các đường cao, bạn sẽ thấy ba đường này sẽ giao nhau tại một điểm duy nhất – điểm này chính là trực tâm. Trực tâm hình học là khái niệm cơ bản người học cần nắm bắt.
- Định nghĩa trực tâm:
- Trực tâm = Giao điểm của ba đường cao trong tam giác.
- Các đường cao: Đoạn thẳng vuông góc từ mỗi đỉnh đến cạnh đối diện.

Nhận thức về trực tâm không chỉ có giá trị trong toán học mà còn trong vật lý, khi mà nhiều mô hình và lý thuyết vận dụng tới kiến thức về hình học. Tìm hiểu về trực tâm trong toán học có thể giúp bạn hiểu sâu hơn về các bài toán hình học.
Tính chất trực tâm
Trực tâm có những tính chất cơ bản rất thú vị và quan trọng. Mỗi đặc điểm này không chỉ giúp chúng ta hiểu về hình học mà còn liên quan mật thiết đến các khái niệm khác.
- Tính chất trực tâm:
- Đồng quy của ba đường cao: Trong mọi tam giác (nhọn, vuông, và tù), ba đường cao luôn cắt nhau tại một điểm gọi là trực tâm.
- Vị trí của trực tâm:
- Trong tam giác nhọn: Trực tâm nằm bên trong tam giác.
- Trong tam giác vuông: Trực tâm trùng với đỉnh góc vuông.
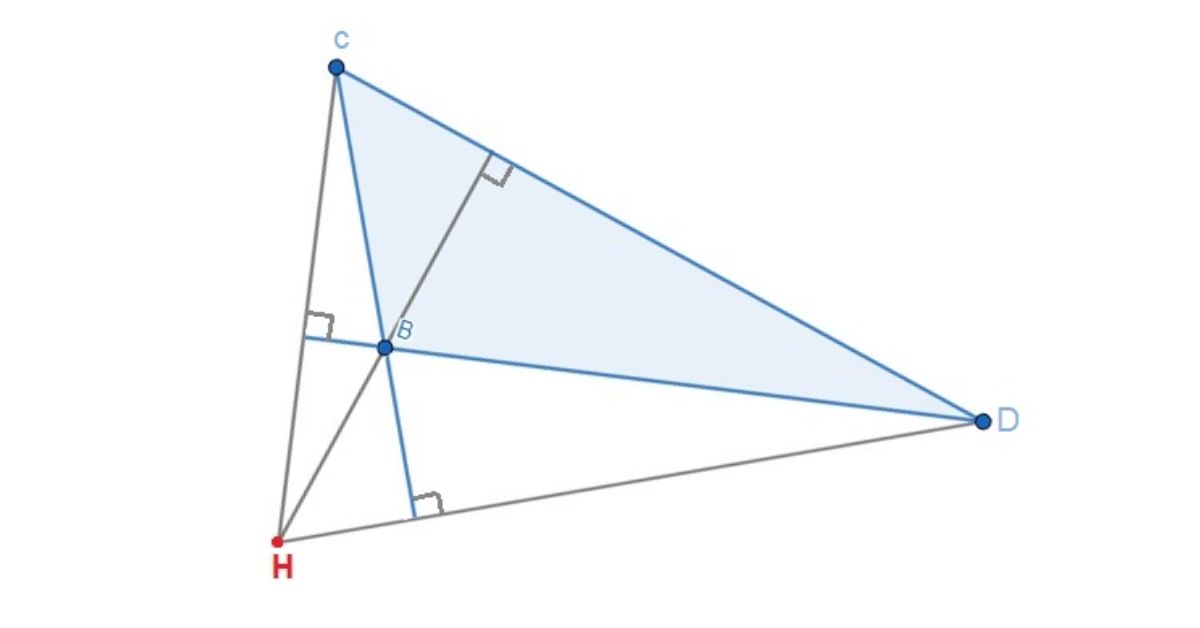
- Trong tam giác tù: Trực tâm nằm bên ngoài tam giác.
- Mối quan hệ với các điểm kỳ diệu khác: Trực tâm có mối liên hệ chặt chẽ với trọng tâm (centroid) và các yếu tố đặc biệt khác trong tam giác. Cả ba điểm này đều nằm trên một đường thẳng gọi là đường thẳng Euler.
Ứng dụng của trực tâm
Trực tâm không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tế trong đời sống hàng ngày.
- Vai trò của trực tâm trong toán học:
- Giúp xác định mối quan hệ giữa các đường thẳng đồng quy và hỗ trợ chứng minh các tính chất liên quan đến tam giác và đường tròn.
- Ứng dụng trong kỹ thuật và vật lý:
- Giúp xác định trọng tâm và điểm cân bằng của vật thể trong thiết kế công trình.
- Làm cơ sở cho phân tích phương tác dụng lực và giải quyết các bài toán liên quan đến cân bằng cơ học. Việc hiểu rõ về trực tâm trong vật lý có thể ứng dụng trong nhiều lĩnh vực khác nhau.
Cách tìm trực tâm
Việc xác định trực tâm của một tam giác có thể thực hiện theo nhiều cách. Dưới đây là các phương pháp cụ thể:
- Cách tìm trực tâm:
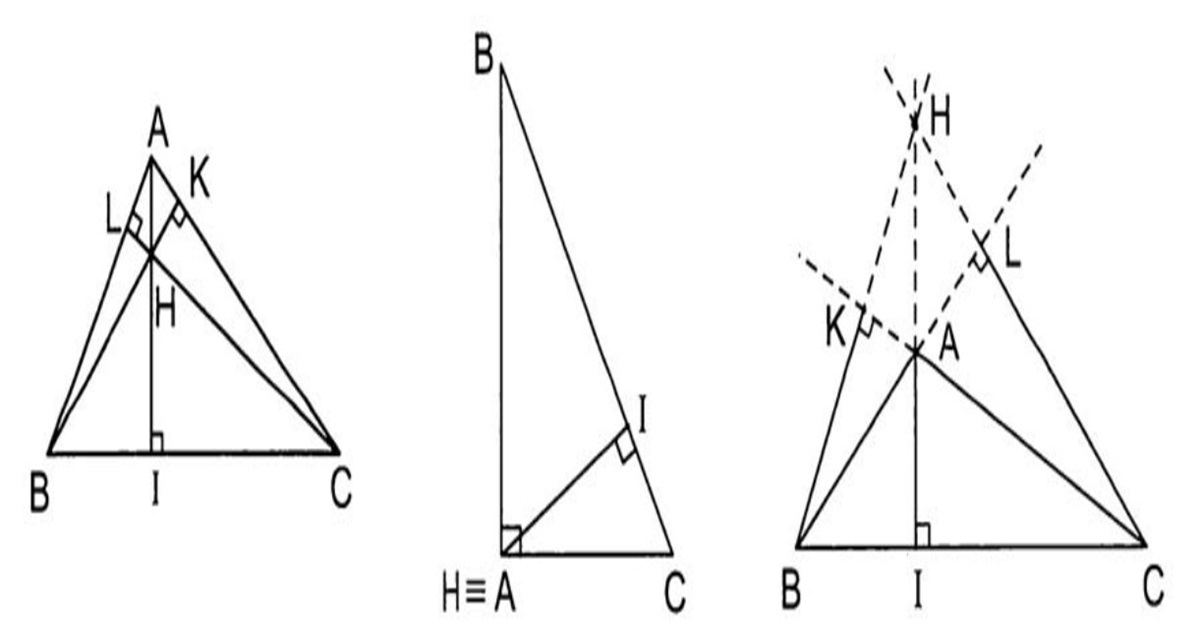
- Tam giác nhọn: Kẻ hai đường cao từ hai đỉnh đến hai cạnh đối diện; điểm giao của hai đường này là trực tâm.
- Tam giác vuông: Trực tâm trùng với đỉnh góc vuông, điều này rất đơn giản khi xác định.
- Tam giác tù: Kẻ đường cao và mở rộng các cạnh nếu cần; giao điểm của chúng sẽ nằm ngoài tam giác.
Các loại trực tâm
Trong hình học, có nhiều loại trực tâm khác nhau tùy thuộc vào các loại tam giác.
- Phân loại các loại trực tâm:
- Trực tâm trong tam giác nhọn, vuông và tù có sự khác biệt rõ rệt về vị trí cũng như cách xác định.
- Điều này đã tạo ra sự phong phú cho việc so sánh và đối chiếu các loại trực tâm trong các hình khác nhau.
Ví dụ minh họa
Để dễ dàng hơn trong việc hiểu rõ trực tâm, dưới đây là hai ví dụ cụ thể:
- Ví dụ 1: Tìm trực tâm của tam giác ∆ABC có các tọa độ A(-2, 6), B(-2, 9), và C(9, 8). Bằng cách tính toán, bạn có thể xác định ra tọa độ của trực tâm H.
- Ví dụ 2: Trong trường hợp tam giác vuông, trực tâm chính là đỉnh góc vuông, điều này giúp người học dễ dàng xác định trong nhiều bài toán. Mối quan hệ giữa trực tâm và centroid cũng chứng minh sự thú vị trong các khái niệm này.
Mối quan hệ giữa trực tâm và trọng tâm
Trực tâm và trọng tâm là hai khái niệm quan trọng trong hình học với sự khác biệt và tương đồng rõ rệt.
- Sự khác biệt:
- Trực tâm là giao điểm của ba đường cao, còn trọng tâm là giao điểm của ba đường trung tuyến.
- Bảng so sánh:
Thuộc tính Trực tâm Trọng tâm Định nghĩa Giao điểm của ba đường cao Giao điểm của ba đường trung tuyến Vị trí Bên trong, ngoài tam giác hoặc tại góc Luôn nằm trong tam giác Liên hệ đặc biệt Thuộc đường thẳng Euler Cũng thuộc đường thẳng Euler
Trực tâm trong hình học không gian
Không chỉ giới hạn trong mặt phẳng, khái niệm trực tâm còn có thể được mở rộng ra hình học không gian.
- Trực tâm trong hình học không gian:
- Khái niệm về trực tâm cũng có thể áp dụng cho các hình khối như hình chóp hay hình cầu.
- Hãy xem xét trường hợp của một hình chóp tam giác, nơi có thể có nhiều điểm tương tự như trực tâm trong không gian ba chiều.
Kết luận
Tóm lại, trực tâm là một khái niệm cơ bản nhưng cực kỳ quan trọng trong hình học. Hiểu biết về trực tâm không chỉ giúp bạn giải quyết các bài toán một cách hiệu quả mà còn mang lại kiến thức áp dụng trong nhiều lĩnh vực khác nhau. Việc掌握 kiến thức về trực tâm sẽ hỗ trợ bạn rất nhiều trong sự nghiệp học tập cũng như trong những ứng dụng thực tiễn trong cuộc sống. Như vậy, việc học hỏi và thực hành với những kiến thức về trực tâm là điều cần thiết cho bất kỳ ai yêu thích toán học và vật lý.

